C++ - 부호비트와 시프트 연산

2. 부호비트와 시프트 연산

    수치 데이터를 저장하는 데이터 타입에는 부호가 있는 데이터와 부호가 없는 데이터가 있습니다. 

    부호가 없는 데이터 값을 시프트 연산하는 것과 달리 부호가 있는 데이터 값을 시프트 연산할 때에는

    부호비트에 따라 연산 과정이 조금 달라집니다.

    2.1 부호비트와 왼쪽 시프트 연산(Left - Shift)

        왼쪽으로 시프트 연산을 수행하는 경우 값은 2배씩 증가하게 됩니다. 이때 아래의 그림과 같이

        최상위 비트와 그 다음 비트가 서로 다른 값인 경우 오버플로우(Overflow)가 발생합니다.

        

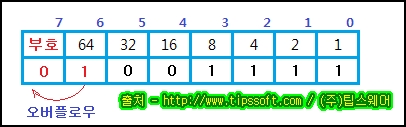
        위의 그림이 왼쪽 시프트 연산을 하기 전 값은 79 이지만 "79 << 1" 을 연산한 결과는 "10011110" 이

        되며 10진수로 변환한 결과 값은 -98이 됩니다. 최상위 비트가 부호비트가 아니라면 연산 결과는

        79 의 2 배인 158 이지만 최상위비트가  변경되어 오버플로우가 발생하였기 때문에 부호가 바뀌고

        결과 값이 원하는 값과 다르게 나온 것입니다.

        오버플로우는 부호비트가 1 에서 0 으로 변경된 경우에도 발생하며 이 때에는 음수가 양수로 바뀌게

        됩니다. 그러므로 부호가 있는 데이터의 왼쪽 시프트 연산 시에는 오버플로우가 발생할 수 있는

        것을 고려해주어야 합니다.

    2.2 부호비트와 오른쪽 시프트 연산(Right - Shift) 

        오른쪽으로 시프트 연산을 하는 경우는 2의 제곱으로 나누기 연산을 하는 것입니다. 이때 비트들이

        오른쪽으로 이동하면서 생긴 공간은 부호비트의 값으로 채워집니다. 아래의 그림에서는 부호비트가

        1이기 때문에 1로채워지지만 만약 부호비트값이 0이라면 0으로 채워지게 됩니다.

        

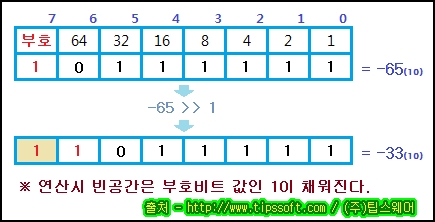
        예를 들어 위의 그림과 같이 "1011 1111" 값을 오른쪽으로 한번 이동하면 왼쪽에 생긴 빈 공간은

        최상위 비트인 1 값으로 채워지는 것입니다. 만약 "-160 >> 4" 를 연산하면 -160 의 이진수 값인

        "1010 0000" 가 오른쪽으로 4비트만큼 이동하고, 왼쪽에 생긴 네개의 빈 공간은 최상위 비트인

        1 로 채워지므로 연산 결과는 "1111 1010" 가 됩니다.